5.10.2 Regress-panel - lineære paneldata-analyser

Linære paneldata-analyser kan gjøres gjennom kommandoen regress-panel. Dette er analyser der den avhengige variabelen er av typen kontinuerlig evt. har rangerbare verdier, f.eks. inntekt eller antall år med utdanning.

NB!

Paneldata-analyser er foreløpig ikke tilgjengelig for modellering av diskrete utfall (logistiske paneldata-analyser).

Syntax:

regress-panel <variabel> <variabelliste> [if <betingelse>] [,<opsjoner>]

Den avhengige variabelen må angis først, etterfulgt av forklaringsvariablene. Opsjoner kan benyttes for ulike formål, som f.eks. robust- eller cluster-estimering, jfr. underkapitlene nedenfor. I likhet med andre statistiske kommandoer, kan også regresjonskommandoer kombineres med en if-betingelse for å kjøre regresjoner på utvalgte grupper. For full oversikt over muligheter, bruk kommandoen help regress-panel.

Se kapittel 2.4 for hvordan en oppretter datasett for paneldata-analyse. Der finner en også et skript-eksempel.

En rekke typer paneldataanalyser kan tas i bruk, avhengig av hvilke antakelser som gjøres om de ulike variablenes variasjon over tid. Vanlige varianter som brukes er "fixed effect"- og "random effect"-analyser. Disse variantene er tilgjengelige gjennom opsjoner:


`fe`	fixed effect	Modell der man kontrollerer for faste individuelle effekter som ikke varierer over tid (within-estimator), gitt ved leddet $\alpha_i$ . Formel: $Y_{it} = \beta_0 + \beta_1 X_{it} + \alpha_i + \epsilon_{it}$ . Modellen fungerer i praksis ved å fjerne individets tidsgjennomsnitt fra alle variabler. Denne "within"-transformasjonen fjerner effektivt den individuelle faste effekten ( $\alpha_i$ ) og alle tidsuavhengige variabler (f.eks. kjønn), som da ikke lenger kan estimeres (estimatet vil da stå som blankt/missing for de aktuelle variablene). Estimatene viser derfor kun effekten av endringer i forklaringsvariablene på endringer i den avhengige variabelen over tid. Fast effekt-modellen estimerer $\beta_1$ ved å se på: "Når $X$ endres, hvor mye endres $Y$ for det samme individet?" (Individet fungerer som sin egen kontroll.) Ved å gjøre dette fjerner den påvirkningen fra de faste, uobserverte individuelle egenskapene ( $\alpha_i$ ). Eksempel på analyse: Estimering av effekt av endring i arbeidserfaring på endring i lønn, kontrollert for uobserverte faste personlighetstrekk. `fe` brukes som standard dersom ingen modellopsjoner velges.
`re`	random effect	I likhet med en fixed effect modell, kontrolleres det også her for faste individuelle effekter som ikke varierer over tid, gitt ved leddet $\mathbf{u_i}$ . Men $\mathbf{u_i}$ antas å følge normalfordelingen $N(0, \sigma^2_u)$ , altså at den faste individuelle effekten i gjennomsnitt er lik 0, og fungerer som en tilfeldig avvikskomponent fra et felles konstantledd ( $\beta_0$ ). Formel: $Y_{it} = \beta_0 + \beta_1 X_{it} + \mathbf{u}_{i} + \epsilon_{it}$ . Det antas dessuten at de uobserverte, individuelle forskjellene ( $\mathbf{u_i}$ ) er ukorrelert med forklaringsvariablene ( $\mathbf{X}$ ). Derfor kan disse forskjellene inkluderes i feilleddet, og modellen estimeres med Generaliserte Minste Kvadraters Metode (GLS). Både variasjon mellom individer og innenfor individer brukes til å estimere koeffisientene, noe som gjør estimatet mer effisient (mindre varians). Dette betyr at variabler som er konstante over tid (f.eks. kjønn) kan estimeres. Random effekt-modellen estimerer $\beta_1$ ved å se på: "Når $X$ endres over tid, og når individer med høyere $X$ har høyere $Y$ , hvor mye endres $Y$ ?" Den antar at de uobserverte forskjellene mellom individer (f.eks. personlighet) ikke er en kilde til skjevhet (bias) i estimatet, men kun en del av feilvariansen. Eksempel på analyse: Estimering av effekt av utdanningsnivå (konstant) og inntekt (varierer) på helse, forutsatt at uobserverte forskjeller mellom individer ikke skaper bias?
`be`	between effect	En mindre brukt modell der man benytter gjennomsnittet av alle variabler målt over tid, inkludert den avhengige variabelen (between-estimator). Formel: $\mathbf{\bar{Y}_{i} = \beta_0 + \beta_1 \bar{X}_{i} + \bar{\mathbf{v}}_{i}}$ . Man estimerer altså tverrsnittsvariasjon basert på gjennomsnittsverdier målt over tid. Modellen fungerer i praksis gjennom å først beregne gjennomsnittet over tid for alle variabler for hvert individ. Deretter utføres en vanlig OLS-regresjon på disse gjennomsnittene. Dette ignorerer all endring over tid (within-variasjonen) og estimerer effekten av forskjeller i $\mathbf{X}$ mellom individer på forskjeller i $\mathbf{Y}$ . Estimatorens koeffisienter er kun konsistente hvis de individuelle effektene er ukorrelert med regressorene, slik som i RE-modellen. Eksempel på analyse: Estimering av effekt av en bedrifts gjennomsnittlige investering over 10 år på dens gjennomsnittlige lønnsomhet.
`pooled`	pooled	Modell der man ser bort fra tidseffekter, og betrakter paneldatasettet som et vanlig tverrsnittsdatasett (pooled-estimator). Man kjører altså en vanlig lineær regresjon (OLS) på et paneldatasett. Hvert individ vil da være representert flere ganger avhengig av antallet målinger. Formel: $Y_{it} = \beta_0 + \beta_1 X_{it} + \epsilon_{it}$

Valget mellom de vanligste modellvariantene FE og RE gjøres ofte ved hjelp av en Hausman-test, som tester antagelsen om at $\alpha_i$ er ukorrelert med $X_{it}$ . Hvis testen avviser nullhypotesen (korrelasjon foreligger), foretrekkes FE-modellen for å unngå skjevhet (bias). Kommandoen hausman kan brukes til dette.

I eksempelet nedenfor brukes årslønn (årlig lønnsinntekt) som avhengig variabel, og dummyvariabler for hhv. sivilstatus=gift og bosted=oslo brukes som forklaringsvariabler. I tillegg er 5 måletidspunkter benyttet: 31/12 i årene 2011-2015. Populasjon = alle personer som fullførte et masterstudium i løpet av høstsemesteret 2010.

Eksempel 1: Panelregresjon med fixed effects

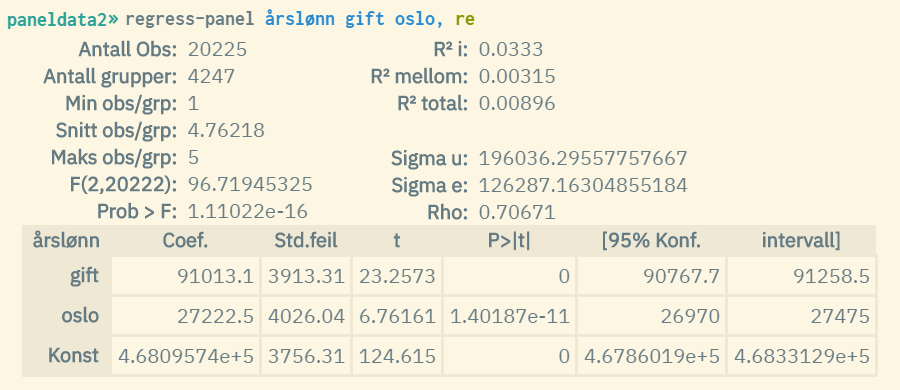
Eksempel 2: Panel-regresjon med random effects (samme datasett som eksempel 1)

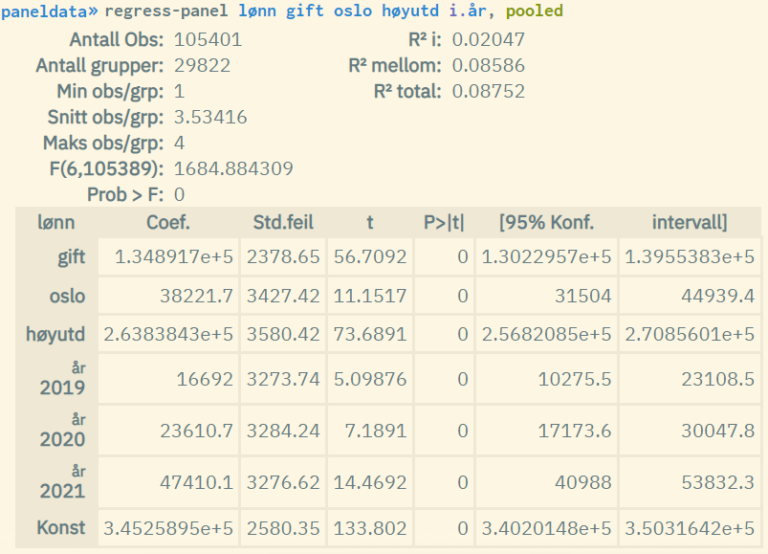
Eksempel 3: "Pooled" panelregresjon

Faktorvariabler, og cluster- og robust-estimering kan også benyttes. Fremgangsmåten er den samme som for ordinær lineær regresjon. Se hhv. kapittel 5.4.1 og 5.4.3 for mer informasjon om dette.

TOLKNING AV MODELLESTIMAT

$R^2$ i = $R^2$ within: Hvor mye av variansen innenfor panelenhetene modellen fanger opp
$R^2$ mellom = $R^2$ between: Hvor mye av variansen mellom panelenhetene modellen fanger opp
$R^2$ total: Den totale $R^2$ måler modellens forklaringskraft og ignorerer eventuelle inkluderte effekter. (Den totale $R^2$ er et vektet gjennomsnitt av de to ovenfor.)
Corr(u_i, Xb): Måler korrelasjonen mellom within enhetsresidual $u_i$ og regressorene i modellen. (Bare rapportert for fixed effect-modeller.)
Sigma u: Standardavvik for residualer innenfor grupper $u_i$ (rapporteres ikke for pooled-modeller)
Sigma e: Standardavvik for residualer (samlet feilledd) $e_{it}$ (rapporteres ikke for pooled-modeller)
Rho: Andel av varians som skyldes $u_i$ (rapporteres ikke for pooled-modeller)

TOLKNING AV KOEFFISIENTESTIMATER

Koeffisientestimatene må tolkes på litt forskjellige måter, avhengig av hva slags modell man kjører:

Modell	Konstantleddet	Koeffisienter
FE	Gjennomsnittet av alle de individuelle, faste $\alpha_i$ -estimatene.	Effekten av en endring i X på endring i Y innenfor det samme individet over tid.
RE	Forventet Y når alle X'er er lik 0, for et gjennomsnittlig individ i populasjonen (det felles senterpunktet for alle $\mathbf{u_i}$ 'ene).	Den vektede effekten av en enhetsøkning i X på Y, basert på både variasjon mellom og innenfor individer.
BE	Forventet gjennomsnittlig Y når alle gjennomsnittlige X'er er lik 0 (det felles gjennomsnittlige nivået).	Den langsiktige effekten av en enhets forskjell i gjennomsnittlig X på gjennomsnittlig Y mellom individer.
Pooled / OLS	Forventet Y når alle X'er er lik 0.	Den generelle effekten av en enhets økning i X på Y på tvers av hele datasettet.

Hvorfor vises ikke koeffisientestimater for tidskonstante opplysninger ved bruk av fixed effekt (fe)?

Når man utfører en panelanalyse med fast effekt-estimering, benyttes en teknikk som fjerner effekten av tidskonstante variabler. Det at estimatene for de tidskonstante variablene ikke vises i resultatene skyldes at de er fjernet i fast effekt-estimeringen. Dette skjer fordi modellen antar at disse effektene er fanget opp i feilleddet, og dermed ikke påvirker estimatene for de andre koeffisientene. Enkelt sagt, det man er interessert i gjennom fast effekt estimering er effekten av variabler som endrer seg over tid, ikke de som er konstante.

$\rhd$ Praktisk eksempel på paneldata-analyse